New paper from the lab accepted at NeurIPS: “Implicit variance regularization in non-contrastive SSL.” In our article, first-authored by Manu and Axel, we add further understanding to how non-contrastive self-supervised learning (SSL) methods avoid collapse.

Preprint: https://arxiv.org/abs/2212.04858
Code: https://github.com/fmi-basel/implicit-var-reg

Self-supervised learning methods like BYOL and SimSiam learn representations by requiring network outputs for two augmented versions of the same input to be similar. However, how these approaches avoid representational collapse still is still not fully understood. In previous work, Tian, Chen, and Ganguli (2021) performed a comprehensive analysis for the Euclidean metric. However, state-of-the-art SSL approaches use the cosine similarity.

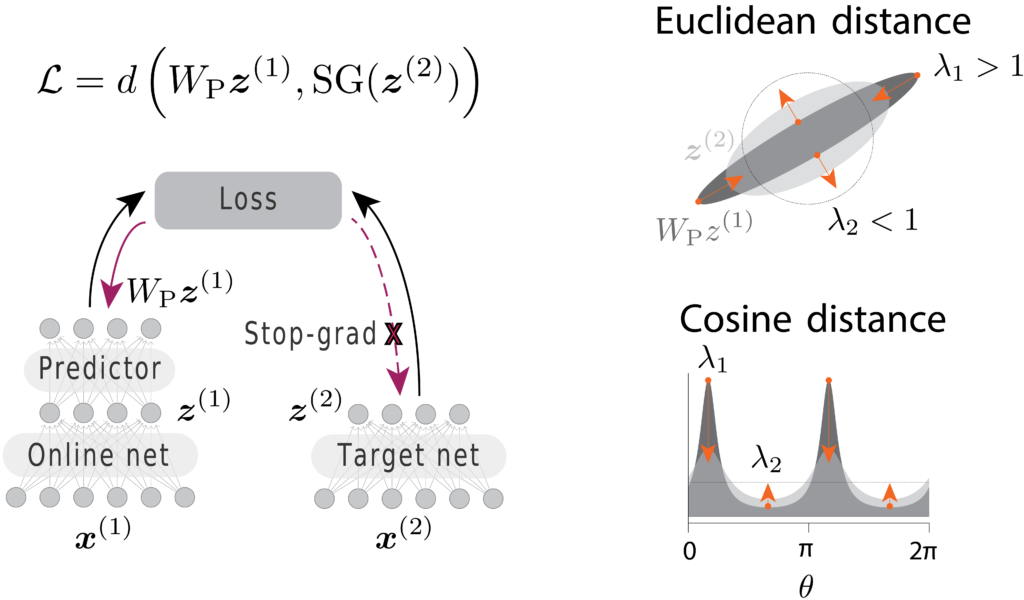
Building on DirectPred (Tian, Chen, and Ganguli 2021), we analyzed the learning dynamics under cosine similarity in the eigenspace of the predictor network. We show that both Euclidean and cosine similarity avoid collapse through implicit variance regularization, albeit through different mechanisms. Our work thereby links DirectPred with VICReg (Bardes, Ponce, and LeCun 2022), which uses explicit variance regularization.

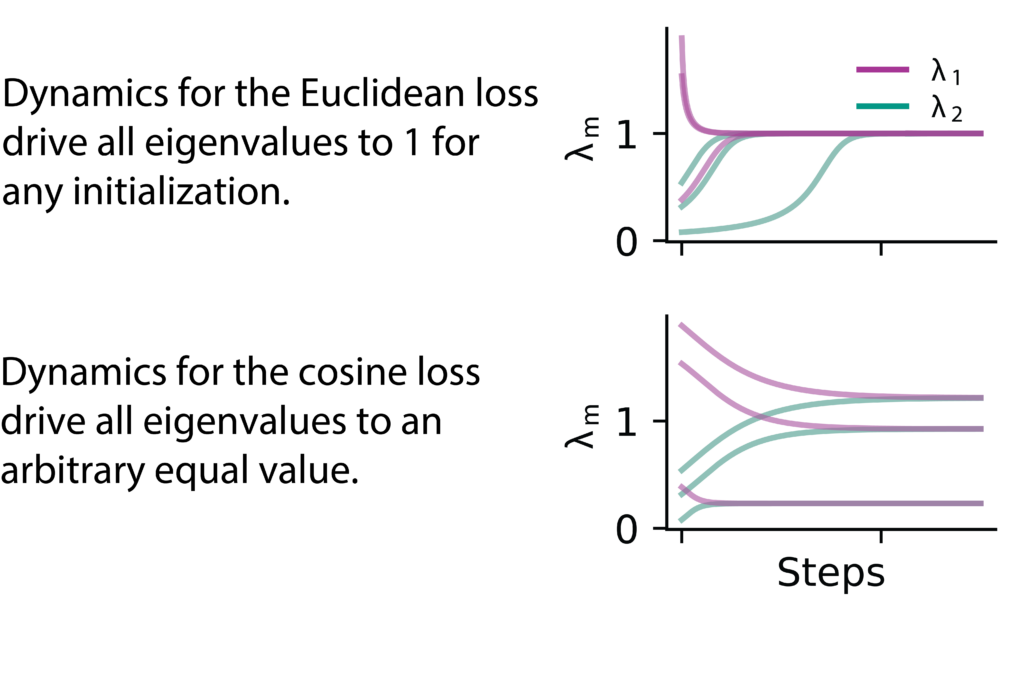
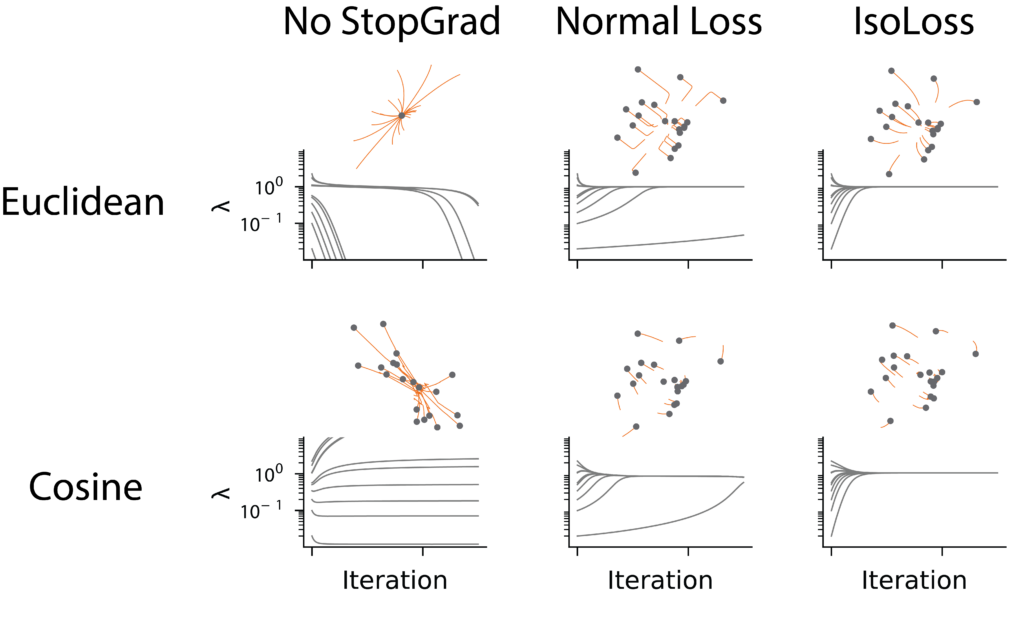
Moreover, our analysis reveals that the eigenvalues of the embedding covariance matrix act as effective learning rate multipliers, which impedes the recruitment of small eigenvalues and leads to low-rank representations. We propose a family of isotropic loss functions that equalize the learning dynamics across modes and show in simulations that IsoLoss speeds up learning and increases robustness, which allows it to dispense with the EMA target.