 Please try this at home!
Please try this at home!
I just put up a beta version of a tutorial showing how to train spiking neural networks with surrogate gradients using PyTorch:
https://github.com/fzenke/spytorch
Emre, Hesham, and myself are planning to release a more comprehensive collection of code in the near future to accompany our tutorial paper. Stay tuned!
Is this implementation the same as that on https://github.com/fzenke/pub2018superspike ?
Is it known if it’s faster/slower than the original implementation?
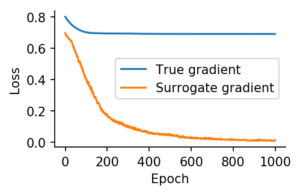
This tutorial implementation is quite different from SuperSpike. Most importantly, it uses a different cost-function and back-end library. This tutorial version illustrates how to use surrogate gradients in modern ML auto-diff frameworks. Whereas SuperSpike is a fully online algorithm running on top of an event-based spiking neural network library. Since SuperSpike is normally used with a van Rossum distance loss to predefined target spike trains the present tutorial uses a crossentropy loss to do classification. Therefore both have never been compared directly. I hope that clarifies it.
Great tutorial indeed! Thanks for sharing!
I had two questions:
1.What is the difference between the tensors out and rst. They both seem to be doing the same thing, in what sense are they different?
2. I was also wondering if in order to add the recurrent weight connection would it be enough to add the following term:
new_syn = alpha*syn + h1[:,t] + torch.mm(out, v)
where v has been defined as
v = torch.empty((nb_hidden, nb_hidden), device=device, type=dtype, requires_grad=True)
torch.nn.init.normal_(v, mean=0.0, std=weight_scale/np.sqrt(nb_hidden))
Concerning your first question: “rst”: is computed using a real step function for which the gradient does not flow, whereas “out” implements a surrogate gradient. In PyTorch this is equivalent to explicitly detaching the graph with rst=out.detach(). Ignoring the reset term when computing the surrogate gradient is one of the “tricks of the trade” that improves learning performance substantially.
Concerning you second question: Yes, this should do the trick.