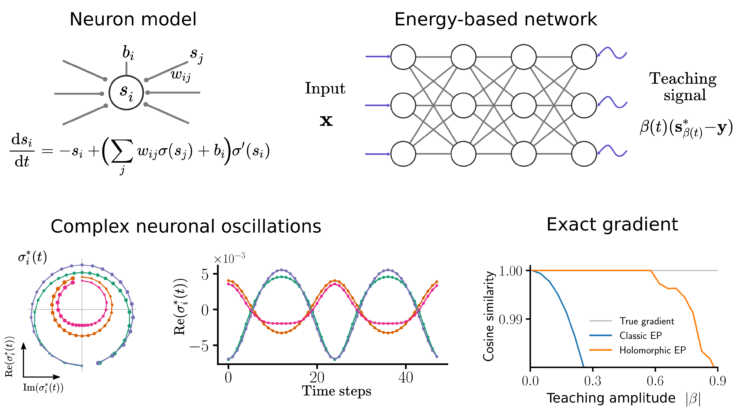
Thrilled to introduce Holomorphic Equilibrium Propagation (hEP) in this new preprint led by Axel Laborieux. We extend classic equilibrium propagation to the complex domain and show that it computes exact gradients with finite size oscillations, thereby linking a solution to the credit assignment problem to local learning rules and oscillations.
Paper: https://arxiv.org/abs/2209.00530
Code: https://github.com/Laborieux-Axel/holomorphic_eqprop
Update (2022-10-06): Now accepted at Neurips.
We show that if the energy function is differentiable with respect to complex variables (“holomorphic”), the gradient is the first Fourier coefficient of neuronal oscillations in the complex plane. These oscillations are caused by a periodic teaching signal at the network’s output.
Importantly, hEP computes exact gradients for large oscillations, in contrast to classic equilibrium propagation which requires small nudges. Large oscillations allow estimating gradients accurately in noisy systems and deep nets where small amplitudes don’t propagate.
We also show that hEP can estimate the gradient online with an always-on teaching oscillation, thereby alleviating the need for precisely timed phases as required in BP and classic EP.
These improvements enable hEP to train deep networks on challenging tasks such as ImageNet 32×32. Moreover, the noise resilience and online capability allow linking hEP to biologically plausible learning rules and developing new training algorithms for neuromorphic hardware.