We are happy our new paper “Improving equilibrium propagation (EP) without weight symmetry through Jacobian homeostasis,” led by Axel accepted at ICLR 2024.

Preprint: https://arxiv.org/abs/2309.02214
Code: https://github.com/Laborieux-Axel/generalized-holo-ep

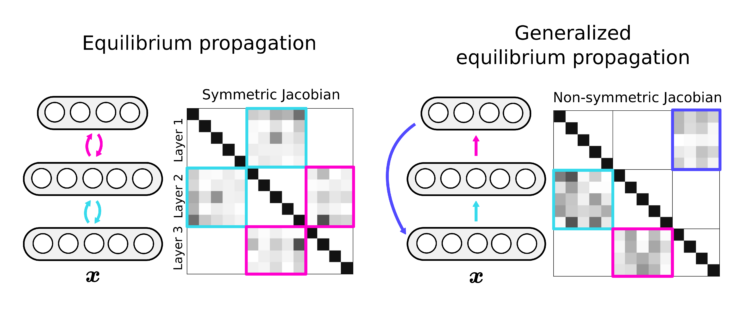
EP prescribes a local learning rule and uses recurrent dynamics for credit assignment. Unfortunately, EP works best in networks with perfect weight symmetry, limiting its utility for studying learning in the brain or training neuromorphic hardware.

To understand how crucial weight symmetry is for EP, we analyzed it in general dynamical systems. We found how finite nudge and non-symmetric weights induce distinct biases in the gradient estimate.

While bias due to finite nudge is avoidable using holomorphic EP, weight asymmetry remains a significant obstacle by inducing non-normal Jacobians. To mitigate this effect, we design a homeostatic loss that encourages symmetry of the Jacobian directly.

Importantly, weight symmetry does not necessarily mean symmetric Jacobian, making Jacobian homeostasis more general than approaches that directly symmetrize the weights, e.g., Kolen & Pollack.

Jacobian homeostasis enables us to train deep networks with untied weights on challenging tasks such as ImageNet 32×32 with minimal drop in accuracy compared to symmetric networks, thereby further strengthening the role of EP family algorithms for bio-plausible learning and neuromorphic engineering.