Surrogate gradients (SGs) are empirically successful at training spiking neural networks (SNNs). But why do they work so well, and what is their theoretical basis? In our new preprint led by Julia, we answer these questions.
Paper: arxiv.org/abs/2404.14964
We studied the relation of SGs with two theoretical frameworks: 1) Smoothed probabilistic models, which provide exact gradients in stochastic neurons. 2) Stochastic autodifferentiation, which deals with derivatives of discrete random variables but hasn’t been applied to SNNs.
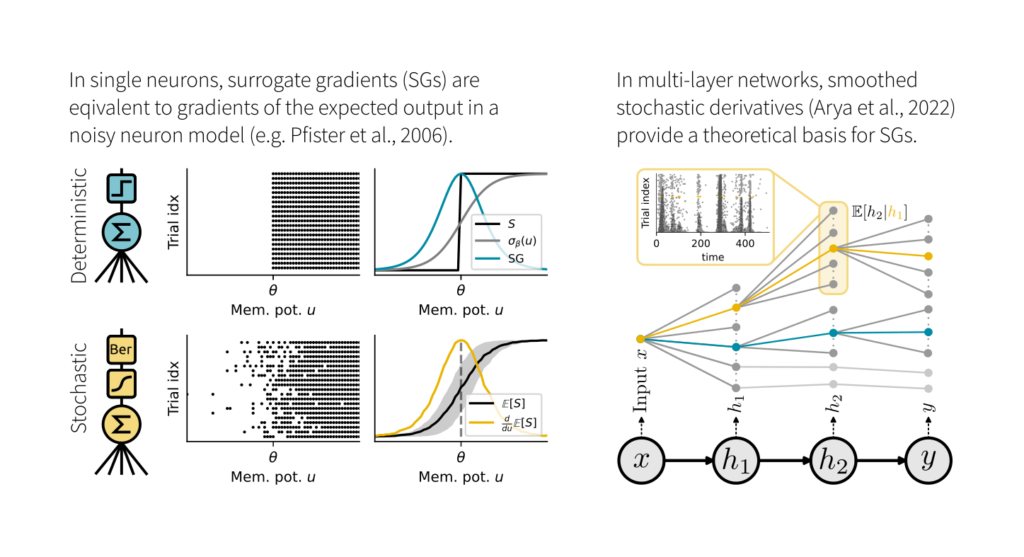
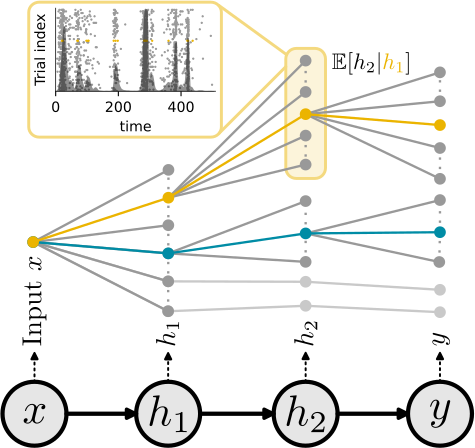
While SGs are equal to the gradient of the expected output in single neurons, this equivalence breaks in deep nets. Here, SGs can be understood as smoothed stochastic derivatives, and the form of the surrogate derivative is linked to the escape noise function of the neurons.
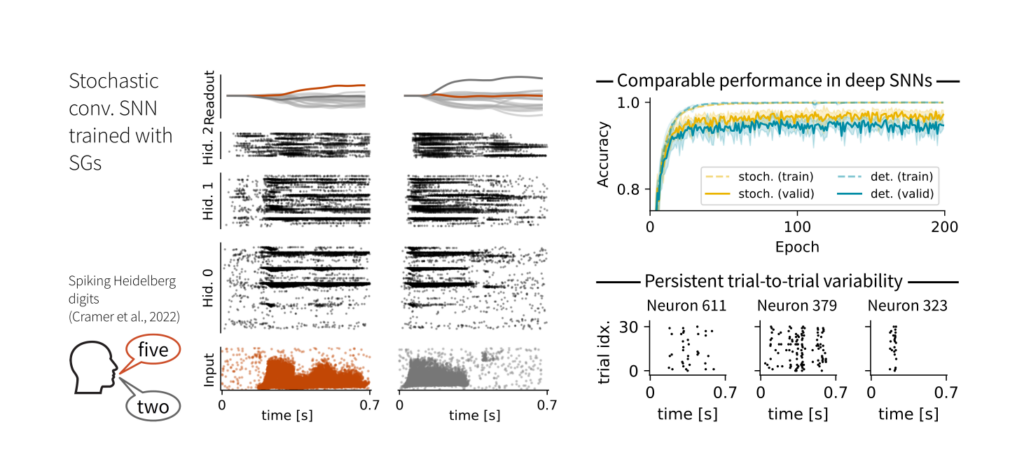
The stochastic motivation makes SGs ideal for training stochastic SNNs. In our experiments, they achieved comparable performance to their deterministic counterparts, albeit with biologically plausible levels of trial-to-trial variability.
Curiously, we also find that we cannot interpret SGs as gradients of a surrogate loss. They do not result in an integral of the closed loop of zero and, therefore, do not correspond to a conservative field.
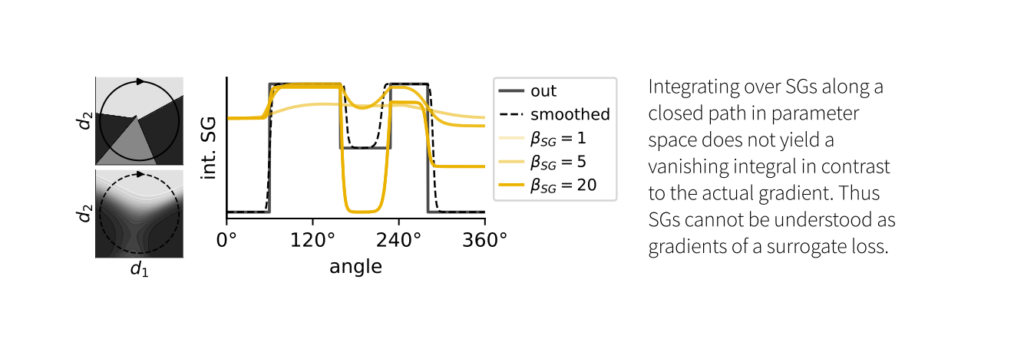
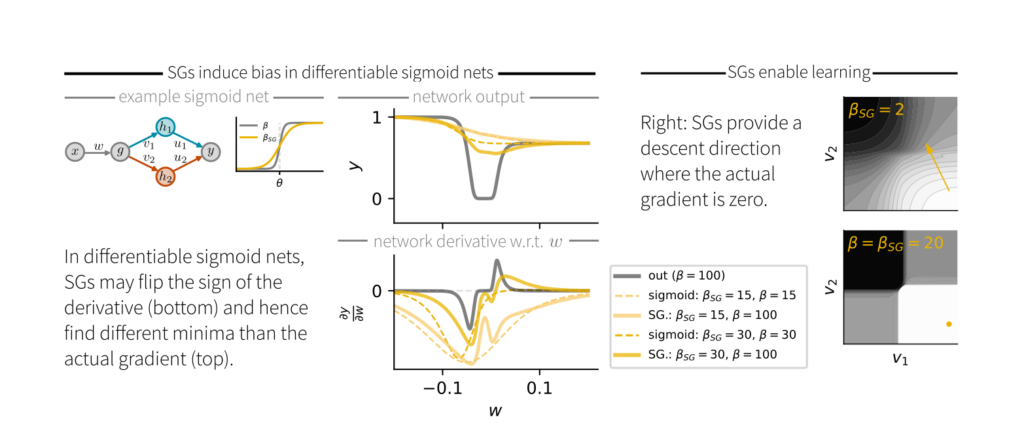
When comparing SGs to actual gradients in differentiable sigmoid networks, we found that the sign of the SG doesn’t always match that of the exact gradient. Consequently, SG descent is not guaranteed to find a local minimum of the loss.