Paper: Finding sparse trainable neural networks through Neural Tangent Transfer

fzenke

New paper led by Tianlin Liu on “Finding sparse trainable neural networks through Neural Tangent Transfer” https://arxiv.org/abs/2006.08228  (and code) which was accepted at ICML. In the paper we leverage the neural tangent kernel to instantiate sparse neural networks before training them.

Deep neural networks typically rely on dense, fully connected layers and dense convolutional kernels. Yet, sparseness holds the potential for substantial savings in terms of their computational cost and their memory requirements. Neurobiology exploits this notion extensively. 

But not all sparse neural networks are created equal, which raises the question as to how to initialize a sparse deep neural network without compromising its performance. Our paper tackles this issue by instantiating sparse neural networks whose training dynamics in function space are as close as possible to a dense net.

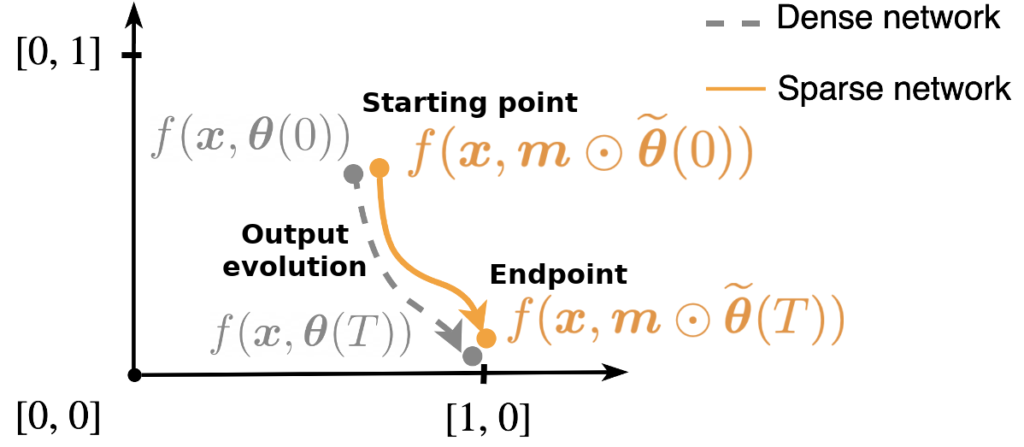
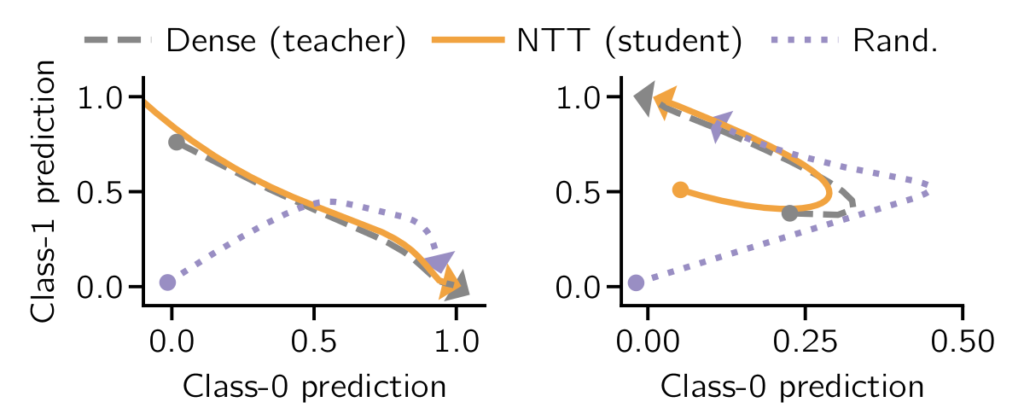
The central idea underlying our approach is that if the starting point and the output evolution are the same, the sparse network will end up at the same endpoint in function space as the dense one.

We achieve this by minimizing the mismatch between the neural tangent kernels of the sparse and an associated untrained dense teacher network. We call this method Neural Tangent Transfer (NTT). Crucially, NTT works without labeled data, and it allows pruning before training as it does not require a trained teacher network.

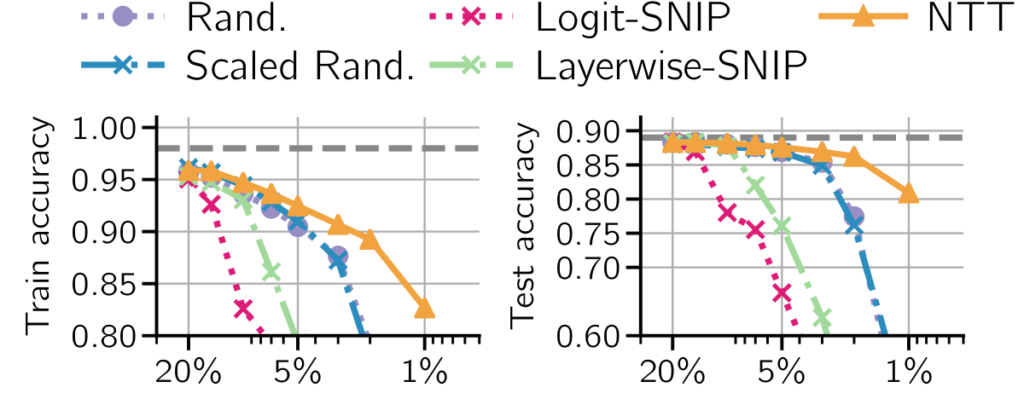
Output evolution during training in a simple 2-way classification network. The trajectory of the randomly pruned network (violet) is markedly different from both the dense teacher (gray) and the sparse student (orange) optimized with our method.

Importantly, NTT outperforms previous approaches in the layer-wise setting by effectively pruning convolutional filters in the lower layers, which contribute most of the computational cost.

Here we plot training and test accuracy of an MLP trained on fashion MNIST as a function of sparseness. Networks optimized with our NTT method (orange) retain higher performance while using fewer parameters.